人は複利を頭で理解できてもイメージできてないとよく言われます。

新聞紙を42回折るとその高さは月まで届きます。実際に折るのは不可能ですが。あくまで計算上。紙を42回折るだけで月まで届くなんて、なかなかイメージできないと思いませんか。私はイメージはできません。でもエクセルで計算したら、確かにそうなります。

複利と同じく、確率も人は理解しているようで実はできてないと言われます。将来、起こり得る事象の確率分布を正確に把握できている人は少ないそうで。

「確率って確かにイメージできてないんだな～」って思わされたのが、モンティ・ホール問題（Monty Hall problem）です。「モンティ・ホール」という名前は知らなくても、問題の内容自体はどこかで聞いたことあるかもしれません。

ウィキペディアから抜粋します。

「プレイヤー（回答者）の前に閉じられた3つのドアが用意され、そのうちの1つの後ろには景品が置かれ、2つの後ろには、外れを意味するヤギがいる。プレイヤーは景品のドアを当てると景品をもらえる。最初に、プレイヤーは1つのドアを選択するがドアは開けない。次に、当たり外れを事前に知っているモンティ（司会者）が残りのドアのうち1つの外れのドアをプレイヤーに教える（ドアを開け、外れを見せる）。ここでプレイヤーは、ドアの選択を、残っている開けられていないドアに変更しても良いとモンティから告げられる。プレイヤーはドアの選択を変更すべきだろうか？」

ウィキペディアより

ドアが3つあります。
3つのドアのうち、1つのドアの後ろに景品があります（アタリ）。
残りの二つのドアの後ろにはヤギがいます（ハズレ）。

あなたはドア１を選んだとします。

ここで、司会者がドア3は不正解（ヤギがいる）と教えてくれたとします。

つまり、こういう状況。


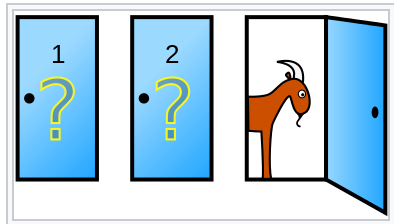
さて、ドア1を選んでいるあなたは、選択肢をドア1のままにしてもいいし、ドア2に変更してもいいです。

あなたならどうしますか？

ドア1のままにします？
それとも、ドア2に変更しますか？

・・・

・・・

ドア1のままでもドア2でも、当たる確率はフィフティ・フィフティだと思いませんか？

実は違うらしいんですよ、これが。

ドア1からドア2に変更した方が、景品が当たる確率は高くなるそうです。ドアを変えると当選確率は2/3になるそうです。

これイメージできます！？

私は無理です。今もまだ理解不能。ドア2に変更した方が景品が当たる確率が高いなんて、全く以って理解できません。

数学をしっかり勉強している人にとっては普通にわかるもんなのでしょうか。分野としては「条件付き確率」になるそうです。ああ、高校生の時にちょっと勉強した記憶があるな・・。

確率は難しい。モンティ・ホール問題以外でも分かってるつもりで、勘違いしていることがきっとたくさんあるんだろうな～って思います。いつか、モンティ・ホール問題が腑に落ちて理解できる日が来るといいな。

確率の勉強って投資家としても大切だと思います。すごく大切。確率が理解できたからって、決して未来予知ができるわけじゃない。でも、将来起こり得る事象の確率分布を把握することで、長期的にどう平均へ回帰するのかがわかります。