学生の時、一番好きな科目って何でしたか？

私は数学です。そんなめちゃ得意ってわけじゃなかったですが好きでした。数学の好きなところは暗記よりもその場の考える力が重視される点（まあ受験数学は暗記なところもあるけど）。あと、物事を抽象化して数字で表現することがクールでかっこいいな～と思ってました。

抽象化ってカッコイイって思ったんです！
中学生の時は「抽象化」なんて単語知らなかったですが、「あらゆる状況を変数変えるだけで表現できる方程式ってすげえなあ」って思ったんです。それは今思えば抽象化に他なりません。

たとえば単純な話で「健太君が時速20kmの速度で走ると、x時間後には何キロ進んでいるでしょうか？」みたいなやつです。

答えは、y=20xですね。

x=1なら20km
x=2なら40km（←もはやフルマラソン。しかも2時間って早い！）
x=2.5なら50km
x=4なら80km
てな感じで、変数xを変えるだけですぐさま結果が返ってきます。

このような数式での抽象化で最初に習うのは、一次方程式ではないでしょうか。多分中学一年生くらいで習ったような気がします。
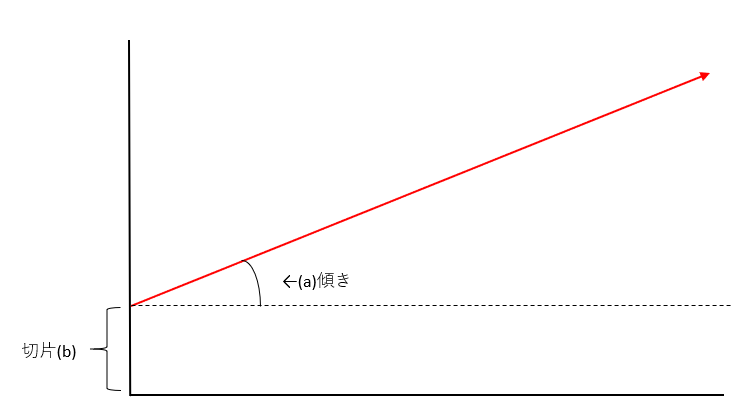
あの”y=ax+b”です。

こんなの見ると吐き気しますか（笑）？
数学って嫌いな人はホント嫌いですよね。

ここから投資の話に繋げたいので、嫌じゃなければこのままお付き合い下さい～。

で、”y=ax+b”の話です。これは一次方程式なわけですが、この式のaとbの名称を覚えていますか？

・・・

aは比例定数、傾き、変化の割合などと呼ばれます。
bは切片です。

覚えてますか？

私は子どもの頃aは「傾き」と呼んでいた記憶があるので、この記事でも「傾き」と言うことにします。bは切片、そのままです。

↑
どうでしょう、思い出しましたか？
こういう関数グラフ、定規を使って頑張ってノートに書きませんでしたか？

 

実は、この中学数学の一次方程式が株式投資で活きるんです！！

私は、長期投資のリターンを想像する時、この一次方程式のグラフを頭に思い描きます。

各銘柄が私に訴えかけてくるんです。
↓こんな感じで。

（ジョンソン＆ジョンソンの訴え）
私の切片は2.7で、傾きは6だよ～。どう買ってみない？

（コカ・コーラの訴え）
俺の切片は3.5で、傾きは4くらいかな～。どう投資しない？

（フェイスブックの訴え）
俺の切片はゼロだけど傾きは10もあるぞ。お買い得だろ？

（AT&Tの訴え）
俺の切片は6.3もあるんだぜ。あ、でも傾きは、、3くらいかな・・。

（マイクロソフトの訴え）
俺の切片は1.5さ。傾きは7くらいは期待してくれ！

、、てな感じです。

意味わかりますか？

私は、
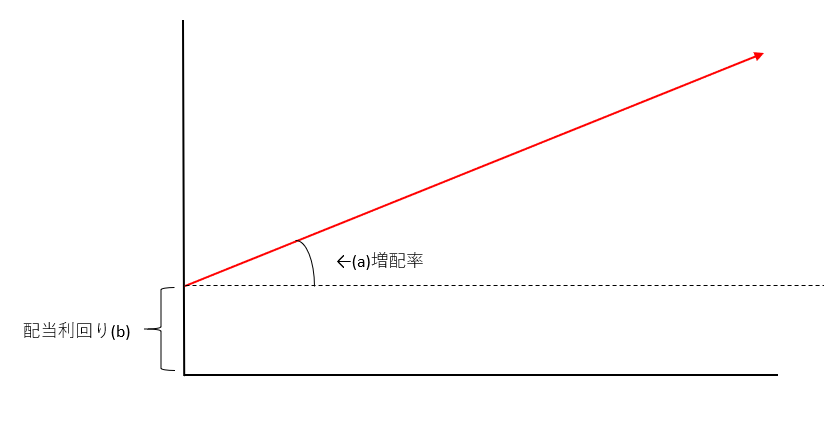
a（傾き）＝DPS成長率（増配率）
b（切片）＝配当利回り
と見ています。

つまり、こういうことです。
（横軸：時間、縦軸：配当）

↑
これをいつも頭に描きながら投資判断しています。ちなみに、実際は配当は複利で成長することが期待されるので、一次関数よりも二次関数で考えるべきかもしれませんが、思考を単純化するため線形の一次関数で考えているまでです。

こうやって、切片(b)＝配当利回りをスタート地点として、将来どれくらい増配していくかな～と思いを巡らせます。

今の配当利回りは調べればすぐにわかることですが、将来の増配率は未知数です。過去の増配実績、最近の業績、ビジネスの将来性などなど、答えはありませんが自分なりに考えてストーリーを思い描きます。「マイクロソフトなら平均して7%の増配率が望めるかな～」などと考えます。

a（傾き）が問題なんです。ここが未来の話なので、誰も正解はわからない。a（傾き）を予想し合っているのが株式マーケットとも言えます。株価はa（傾き）次第ですから。

この傾きをどれくらいで見込むべきか、自分なりに考えます。んで、上のグラフを想像します。

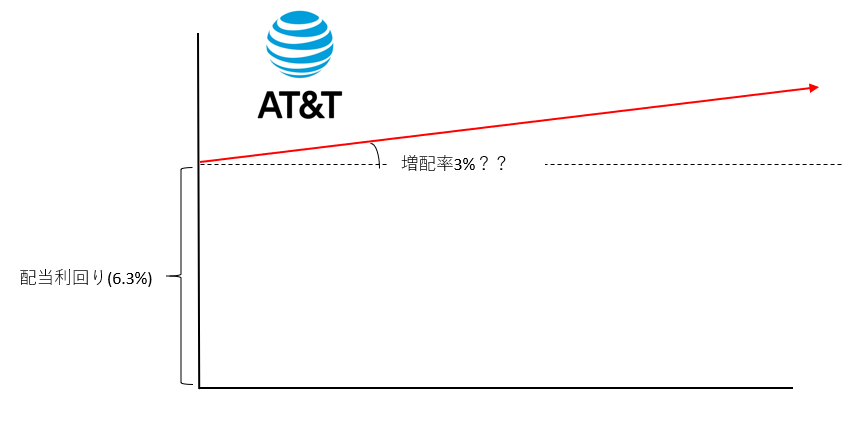
AT&Tとマイクロソフトで具体的に考えてみます。

AT&Tのマイクロソフトの傾き(a)と切片(b)は以下と見込むとします。

（AT&Tの訴え）
俺の切片は6.3(b)もあるんだぜ。あ、でも傾きは、、3(a)くらいかな・・。

（マイクロソフトの訴え）
俺の切片は1.5(b)さ。傾きは7(a)くらいは期待してくれ！

↑
両銘柄に対して、こんなイメージ図を描きます。

どっちの方が長期投資リターンが高いと思いますか？

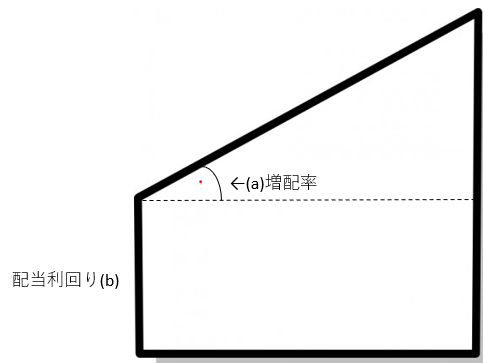
このグラフを描くと台形が出来上がります。
（切片＝配当利回り）を上底とした台形が見えますよね。

こんな感じの。
↑
この面積が超重要です。この面積があなたの累積投資リターンを示しています。

増配率(a)も大事だし、配当利回り(b)も大事。どちらも大きいに越したことはありません。配当利回りが高く、かつ増配率まで高い銘柄があればサイコーです。でも、現実的にそんな銘柄はありません。

AT&Tは配当利回りは6%以上もあって高いけど、将来の大きな増配は期待できません。最近の増配率は2%ちょいでインフレをカバーできる程度です。一方で、マイクロソフトは配当利回りは1.5%とS&P500より低いですが、業績絶好調で今後も大きな増配が期待できそうです。

AT&T、マイクロソフトどちらに投資するのが正解なのか答えはわかりません。

ただ、こうやって一次方程式でグラフを描くと段々と分かってくることがあります。

それは、投資期間が長期になればなるほど(b)切片＝配当利回りよりも、(a)傾き＝増配率の方が重要になってくるということです。時が経ってずっとグラフの右側に行くに連れて、最初のスタート地点が高いか低いかなんてちっぽけなことになっていきます。

最初のスタート地点が高いか低いか（＝配当利回りが高いか低いか）よりも、いかに大きな傾きで増配していけるかの方が、台形の面積に与えるインパクトが大です。ましてや、現実の企業収益（配当）は一次関数的にではなく、二次関数的（複利）に上昇していくのです。

だから、過度に配当利回りにこだわり過ぎないことです。スタート地点で優位に立とうと思い過ぎないこと。それよりも、将来の増配率（EPS成長率と考えてもよい）を高く維持できるかどうかの方がよほど重要です。